Unit circle fill in quiz – Embark on a captivating journey into the realm of trigonometry with our Unit Circle Fill-In Quiz. Dive into the depths of this enigmatic circle, uncovering its intricate definitions, coordinates, and equations. Prepare to test your knowledge and solidify your understanding of this fundamental concept.
Our comprehensive quiz covers a wide range of topics, ensuring a thorough exploration of the unit circle. From defining its essence to pinpointing coordinates and solving equations, you’ll delve into the heart of trigonometry, unraveling its secrets.
Unit Circle Definitions
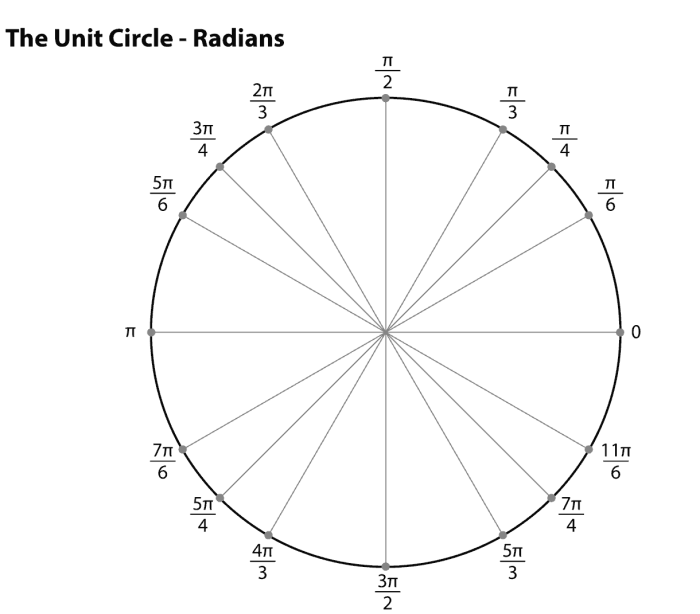
A unit circle is a circle with a radius of 1. It is often used in trigonometry to represent the relationship between the sine, cosine, and tangent of an angle.
Examples of unit circles include:
- The circle with center at the origin and radius 1 in the Cartesian coordinate plane.
- The circle with center at the origin and radius 1 in the complex plane.
The unit circle is closely related to trigonometry. The sine, cosine, and tangent of an angle can be defined as the coordinates of the point on the unit circle that corresponds to that angle.
Relationship to Trigonometry
The unit circle is a useful tool for understanding the relationships between the sine, cosine, and tangent of an angle. For example, the sine of an angle is equal to the y-coordinate of the point on the unit circle that corresponds to that angle.
The cosine of an angle is equal to the x-coordinate of the point on the unit circle that corresponds to that angle. The tangent of an angle is equal to the ratio of the y-coordinate to the x-coordinate of the point on the unit circle that corresponds to that angle.
Unit Circle Coordinates
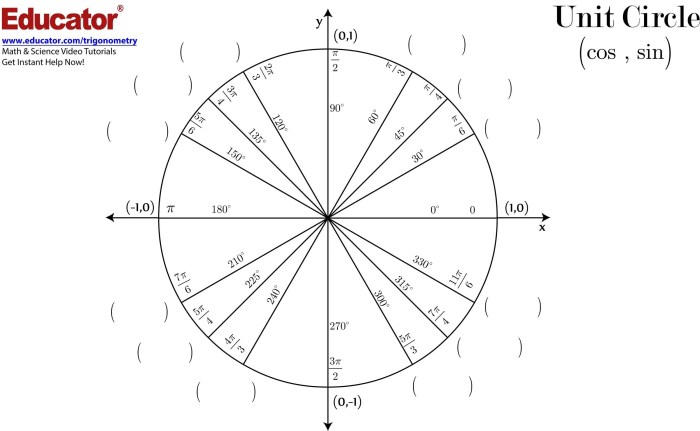
To find the coordinates of a point on the unit circle, we use the angle measure from the positive x-axis. The x-coordinate is the cosine of the angle, and the y-coordinate is the sine of the angle. For example, if the angle is 30 degrees, the x-coordinate is cos(30) = √3/2 and the y-coordinate is sin(30) = 1/2.
The unit circle fill in quiz is a great way to test your understanding of the unit circle. If you’re looking for a fun and engaging way to learn about meiosis, check out oh me oh my oh meiosis . After you’ve mastered meiosis, come back and give the unit circle fill in quiz another try!
Relationship between Coordinates and Angle Measure, Unit circle fill in quiz
The coordinates of a point on the unit circle can be used to determine the angle measure from the positive x-axis. The arctangent of the y-coordinate over the x-coordinate gives the angle measure. For example, if the coordinates are (√3/2, 1/2), the angle measure is arctan(1/2/√3/2) = 30 degrees.
Unit Circle Equations
The equation of the unit circle is a mathematical expression that describes the relationship between the coordinates of any point on the circle and the radius of the circle. The standard equation of the unit circle is:
x^2 + y^2 = 1
where x and y are the coordinates of any point on the circle, and r is the radius of the circle. Since the unit circle has a radius of 1, the equation can be simplified to:
x^2 + y^2 = 1
Using the Equation to Solve Problems
The equation of the unit circle can be used to solve a variety of problems, such as:
- Finding the coordinates of a point on the unit circle given an angle.
- Determining the distance between two points on the unit circle.
- Finding the area of a sector of the unit circle.
Relationship between the Equation and the Properties of the Unit Circle
The equation of the unit circle is closely related to the properties of the unit circle. For example, the equation shows that the unit circle is a circle with a radius of 1. It also shows that the center of the unit circle is at the origin (0, 0). Additionally, the equation can be used to derive other properties of the unit circle, such as the fact that the circumference of the unit circle is 2π.
Unit Circle Fill-in Quiz
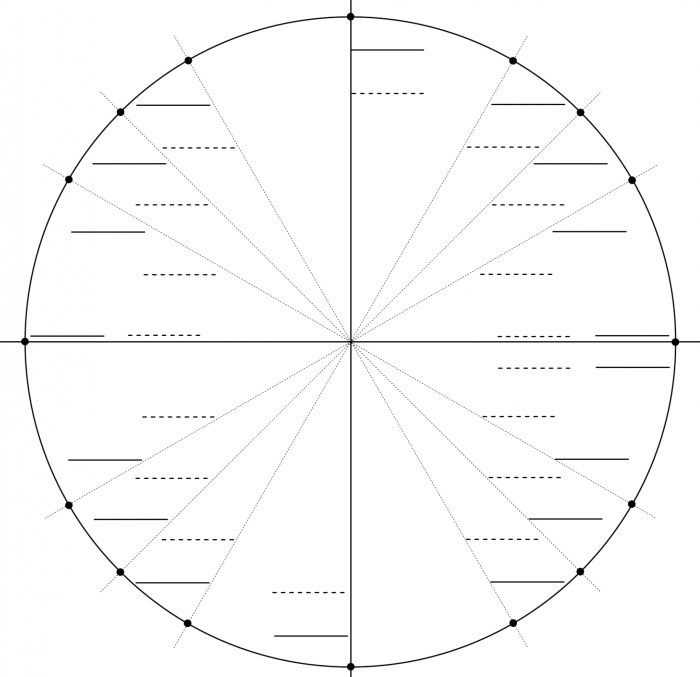
Test your knowledge of the unit circle with this comprehensive fill-in quiz. The quiz covers various aspects of the unit circle, including definitions, coordinates, and equations.
Definitions
- The unit circle is a circle with a radius of 1.
- The coordinates of a point on the unit circle are (cos(θ), sin(θ)), where θ is the angle between the positive x-axis and the line connecting the point to the origin.
- The equation of the unit circle is x² + y² = 1.
Coordinates
- The point (1, 0) is located on the positive x-axis.
- The point (0, 1) is located on the positive y-axis.
- The point (-1, 0) is located on the negative x-axis.
- The point (0, -1) is located on the negative y-axis.
Equations
- The equation sin(θ) = y/r represents the y-coordinate of a point on the unit circle.
- The equation cos(θ) = x/r represents the x-coordinate of a point on the unit circle.
- The equation tan(θ) = y/x represents the slope of the line connecting a point on the unit circle to the origin.
Questions and Answers: Unit Circle Fill In Quiz
What is the definition of a unit circle?
A unit circle is a circle with a radius of 1.
How do I find the coordinates of a point on the unit circle?
To find the coordinates of a point on the unit circle, use the following equations: x = cos(theta) and y = sin(theta), where theta is the angle measure from the positive x-axis to the point.
What is the equation of the unit circle?
The equation of the unit circle is x^2 + y^2 = 1.