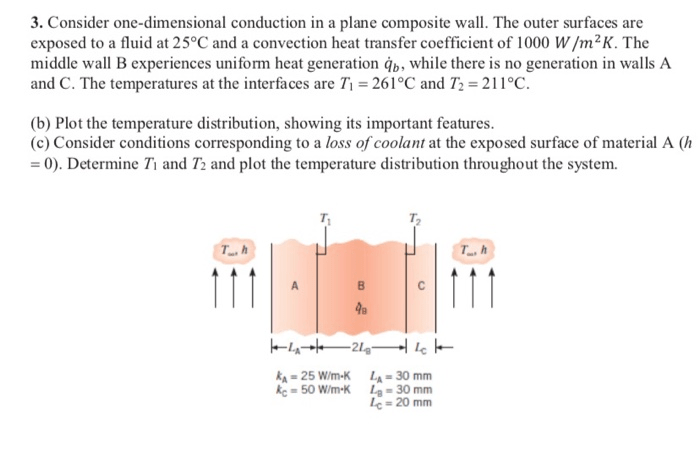
Consider one-dimensional conduction in a plane composite wall, a fundamental concept in heat transfer that governs the flow of thermal energy through complex structures. This comprehensive analysis delves into the governing equation, thermal resistance, heat transfer rate, temperature distribution, and practical applications, providing a thorough understanding of this critical phenomenon.
The governing equation establishes the mathematical framework for analyzing one-dimensional conduction, while thermal resistance quantifies the resistance to heat flow. Understanding the heat transfer rate is essential for predicting the thermal performance of composite walls, and the temperature distribution provides insights into the spatial variation of temperature.
2. Governing Equation
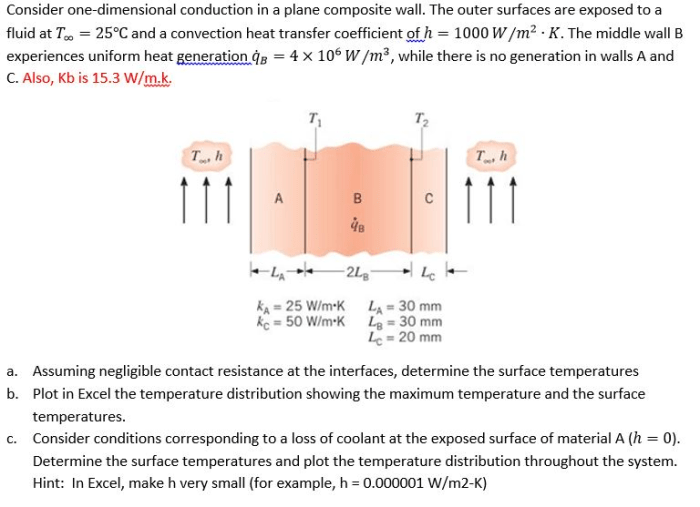
The governing equation for one-dimensional conduction in a plane composite wall is the Fourier’s law of heat conduction, which states that the heat transfer rate is proportional to the temperature gradient and the cross-sectional area of the wall.
Mathematically, it can be expressed as:
$Q =
kA \fracdTdx$
where:
- $Q$ is the heat transfer rate (W)
- $k$ is the thermal conductivity of the wall material (W/mK)
- $A$ is the cross-sectional area of the wall (m 2)
- $\fracdTdx$ is the temperature gradient (K/m)
The governing equation is significant because it provides the mathematical framework for analyzing heat transfer through plane composite walls.
3. Thermal Resistance
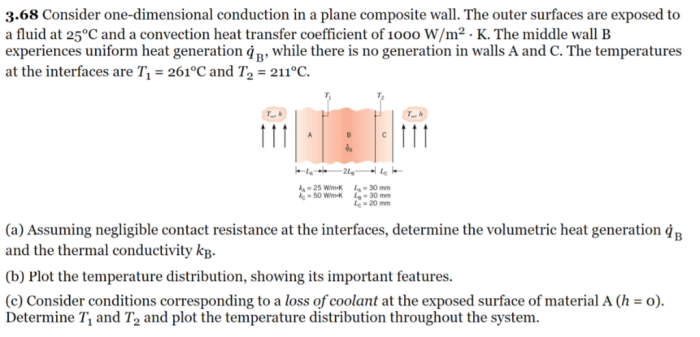
Definition
Thermal resistance is a measure of the resistance to heat flow through a material. It is defined as the temperature difference between the two surfaces of the material divided by the heat transfer rate.
Concept in a Plane Composite Wall
In a plane composite wall, the thermal resistance is the sum of the thermal resistances of the individual layers of the wall.
Calculation
The thermal resistance of a plane composite wall can be calculated as:
$R = \sum_i=1^n \fracL_ik_i A$
where:
- $R$ is the thermal resistance (K/W)
- $L_i$ is the thickness of the $i$th layer (m)
- $k_i$ is the thermal conductivity of the $i$th layer (W/mK)
- $A$ is the cross-sectional area of the wall (m 2)
- $n$ is the number of layers in the wall
4. Heat Transfer Rate: Consider One-dimensional Conduction In A Plane Composite Wall

Calculation
The heat transfer rate through a plane composite wall can be calculated using the following equation:
$Q = \fracT_1
T_2R$
where:
- $Q$ is the heat transfer rate (W)
- $T_1$ is the temperature of the hot surface (K)
- $T_2$ is the temperature of the cold surface (K)
- $R$ is the thermal resistance of the wall (K/W)
Factors Affecting Heat Transfer Rate
The heat transfer rate is affected by the following factors:
- Temperature difference between the hot and cold surfaces
- Thermal conductivity of the wall material
- Thickness of the wall
- Cross-sectional area of the wall
Relationship between Thermal Resistance and Heat Transfer Rate, Consider one-dimensional conduction in a plane composite wall
The heat transfer rate is inversely proportional to the thermal resistance. This means that a higher thermal resistance will result in a lower heat transfer rate.
Common Queries
What is the significance of thermal resistance in a plane composite wall?
Thermal resistance represents the resistance to heat flow through the wall. It is a crucial parameter for determining the heat transfer rate and temperature distribution.
How does the heat transfer rate vary with thermal resistance?
The heat transfer rate is inversely proportional to the thermal resistance. A higher thermal resistance results in a lower heat transfer rate.
What factors influence the temperature distribution in a plane composite wall?
The temperature distribution is affected by the thermal conductivity of the materials, the wall thickness, and the boundary conditions.